算法导论(Introduction to Algorithm)第13章详细介绍了红黑树的定义和具体的操作,这里记录下结合实际的红黑数实现(Java TreeMap)对这一数据结构的理解。
定义
红黑树(Red-Black Tree)是一类排序二叉树,和普通的二叉查找树不同,对红黑树中的每个节点来说,除了基础的左右节点信息、值信息之外,增加了额外的颜色信息。在此基础之上,红黑树增加了一些额外的条件约束,以此来保证树的平衡性。具体的条件是,
- 节点或者是黑色或者是红色
- 根节点是黑色
- 空的叶节点是黑色
- 如果一个节点是红色,则它的左右子节点都是黑色
- 每一个节点到其后继的每个叶节点之间包含相同数量的黑色节点
这几个条件约束保证了红黑树的高度不超过2lg(n-1),n为节点数。
在进行树的结构变动时,均需要注意是否违背了上述定义。当出现与定义不一致的情况,就需要进行调整。调整的手段有,
- 改变节点颜色
- 节点旋转(左旋、右旋)
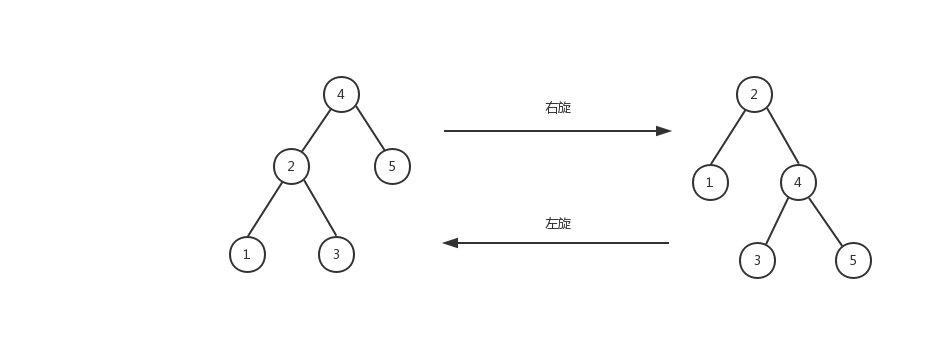
具体结合节点增删时候的代码来进行分析在什么场景需要使用什么操作。
增加节点
流程
红黑树首先要满足排序二叉树的要求,而后再满足其自身定义的约束。节点增加的步骤可以分为两大块,
- 节点插入,普通二叉查找树逻辑
- 节点调整,调整节点颜色或旋转节点
确定颜色
新节点应该设置什么颜色?
- 红黑树为空。根据条件2,节点设置成黑色。
- 红黑树非空。此时需要根据定义进行分析判定。
- 新节点为黑色,违背条件5,新节点所在路径黑色节点树比其余路径增多了
- 新节点为红色,当父节点为红色时,违背条件4,存在父子节点都为红色情况
当红黑树非空时,将节点设为黑色,会发现整个红黑树节点都需要进行变色或旋转,否则难以满足条件。若设置成红色,则即便存在违背条件4的情况,也可以在局部进行变化,然后层层迭代处理。因此,可以得到初步结论,
- 红黑树非空。节点设置成红色。
变色旋转
接下来就考虑一下新节点为红色时存在的情况。
- 如果父节点为黑色,则符合定义,不用任何调整。
- 如果父节点为红色,违背条件4,需要对父节点做变色处理。
当父节点从红色变为黑色之后会出现的情况是,父节点到其后继子节点路径上的黑色节点数量增加了1,为了满足条件5,需要通过变化将父节点到后继子节点路径上的黑色节点数量减少1,以此来保持平衡。
如何进行处理?假设红黑树中存在如下子结构,
场景一,节点1与其父节点为红色,父友邻节点为红色,则进行如下变化,
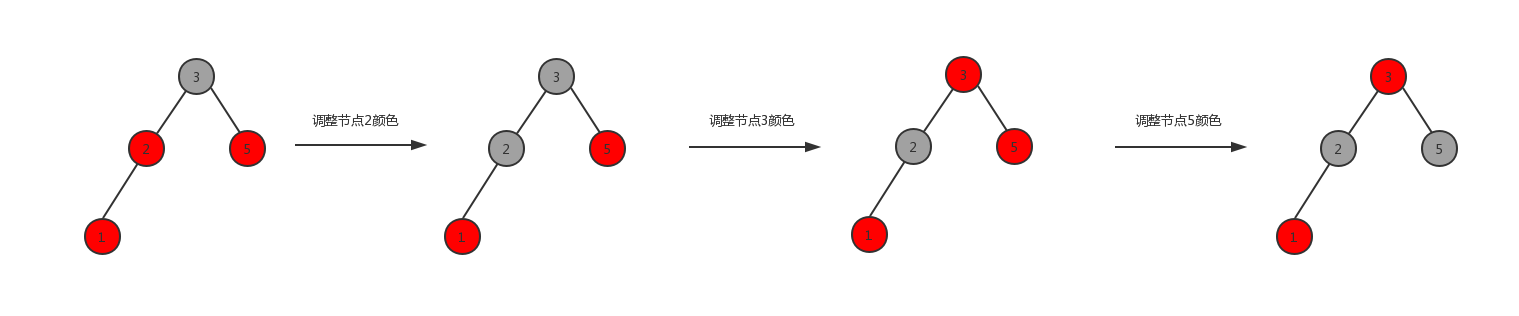
场景二,节点1与其父节点为红色,父友邻节点为黑色,则进行如下变化,

可以看出上图最左与最右的结构,左右路径上的黑色节点数保持不变,同时经过变化也不存在两个相邻的红色节点。
场景一只有变色操作,场景二最后有一步旋转操作。为什么选择这样的操作?
首先新增节点父节点的颜色调整是不可避免的,这就带来了局部路径上黑色节点数增多问题。之后不论是变色还是旋转都是为了将路径中的黑色节点数再减少回去,根据局部结构的不同,选择合适的操作。新增节点为左节点或右节点处理的手段是对称的,这里也不再完全枚举了。
实际的代码,可以看下Java TreeMap中的fixAfterInsertion方法,
移除节点
流程
同样的红黑树的节点移除操作,也分为两大块,
- 节点移除,普通二叉查找树逻辑
- 节点调整,调整节点颜色或旋转节点
移除逻辑
二叉树移除节点过程也简单说明一下,分几种情况,
- 对于叶节点来说,需要将当前节点移除,此外无结构上调整。
- 对于含有一个子节点的节点来说,需要将当前节点移除,同时让父节点指向子节点。
- 对于内部节点来说,不能单纯移除,需要找当前节点的后继节点。将后继节点的值复制当当前节点,移除后继节点。
实际代码可以参考Java TreeMap中的deleteEntry方法。
节点调整
在找到真正需要从结构上进行移除的节点之后,需要开始考虑如何满足红黑树的定义。根据最终待移除的实际节点进行区分,
- 待删除节点为红,移除后不会破坏红黑树条件,无需调整
- 待删除节点为黑,移除后会影响路径上的黑色节点数,需要进行变化处理
考虑几种情况,
- 待删除节点为叶节点
- 待删除节点为中间节点
不论哪种情况实际要解决的就是在路径上黑色节点数减少之后需要再度达成一致。
被移除节点的子树通过调整可以完成的,则在局部进行处理,例如被移除节点的子节点是红色,则直接变为黑色即可。
被移除节点的子树内部不能直接调整完成的,则将问题转移到被移除节点的父节点。如果经过旋转变色之后能够满足条件则处理结束,否则将左右子树路径上的黑色节点调整一致之后,再将问题上抛一层,直至条件满足。
实际的处理过程可以参考Java TreeMap fixAfterDeletion方法。
总结
对红黑树的理解更多还是偏概念上的,之前没有深入了解郭这一数据结构,刚好借着阅读Java代码的机会来看一下这个应用相对广泛的平衡树结构。如果未来什么时候被人问起红黑树的问题,至少不会一点也答不出来了,但要落笔即写对,也并不容易。